Magnetic Resonance Imaging
The classical Magnetic Resonance Tomography (MRT) setup is constructed such that the measurements are approximately described by the Fourier transform of the spin density, which is mainly determined by the hydrogen density. In this model the problem is linear and well-posed, and reconstructions can easily and efficiently be achieved by FFT.
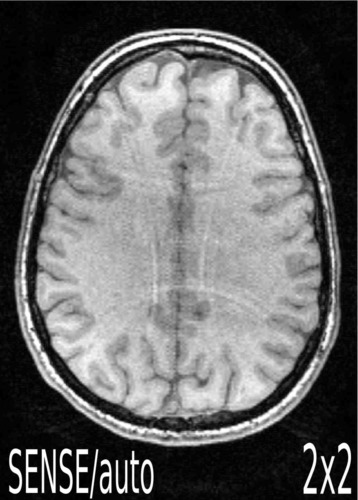
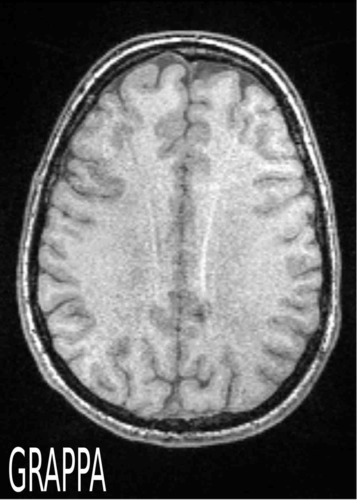
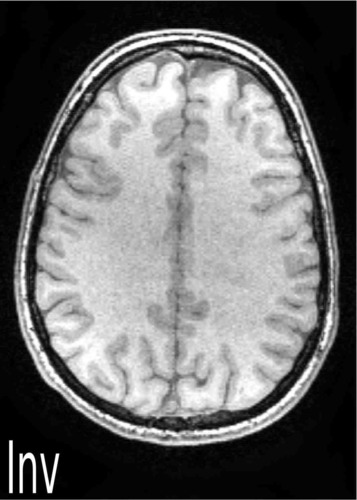
An essential drawback of MRI in comparison to other imaging modalities is the sequential nature of data acquisition, which leads to relatively long measurement times. A certain acceleration can be achieved by parallel measurements with several receiver coils. Here the unknown spin density is multiplied by a space dependent factor called coil profile. Unfortunately, the coil profiles depend on the sample and have to be reconstructed jointly with the sample. This leads to a nonlinear ill-posed problem. In the PhD thesis of Martin Uecker we developed nonlinear iterative inversion methods for this problem, which lead to a substantial improvement of the quality of the reconstructed images compared to widely used reconstruction methods like SENSE and GRAPPA.
Diffusion-MRI allows measurements of the diffusion of water molecules, which are described in some approximation by a 6 dimensional Fourier transform. In the brain diffusion mainly takes place along nerve fibers. Classically, diffusion in each voxel is modelled by a tensor, which is determined by 7 measurements. For reconstructing fiber tracks, this approach leads to difficulties at fiber crossings. A way out is the use of High Angular Resolution Diffusion Imaging (HARDI). The aim is to reconstruct the diffusion strength at each voxel and in each direction. Hence, the unknown orientation distribution function depends on three spatial and two angular variables. In the PhD thesis of Christoph Ruegge we studied special regularization terms which only enforce smoothness along fibers, but not orthogonal to the fibers. By studying the functional analytic properties of the corresponding norms we could in particular establish the regularizing property of the approach.
With the help of orientation distribution functions one can reliably reconstruct fiber tracks even in the presence of crossings. In the PhD thesis of Helen Schomburg we have developed a Bayesian-type semi-local tracking algorithm, in which noise sensitivity is substantially reduced by a combination of extrapolation and a look-ahead strategy. In a stochastic variant we additionally obtain information on the uncertainty of our tracking results.

Currently we are working with Martin Uecker on 2 and 3 dimensional real-time cardiac MRI.
The classical Magnetic Resonance Tomography (MRT) setup is constructed such that the measurements are approximately described by the Fourier transform of the spin density, which is mainly determined by the hydrogen density. In this model the problem is linear and well-posed, and reconstructions can easily and efficiently be achieved by FFT.
An essential drawback of MRI in comparison to other imaging modalities is the sequential nature of data acquisition, which leads to relatively long measurement times. A certain acceleration can be achieved by parallel measurements with several receiver coils. Here the unknown spin density is multiplied by a space dependent factor called coil profile. Unfortunately, the coil profiles depend on the sample and have to be reconstructed jointly with the sample. This leads to a nonlinear ill-posed problem. In the PhD thesis of Martin Uecker we developed nonlinear iterative inversion methods for this problem, which lead to a substantial improvement of the quality of the reconstructed images compared to widely used reconstruction methods like SENSE and GRAPPA.



Comparison between linear reconstruction methods (auto-calibrated SENSE and
GRAPPA) and non-linear reconstruction at subsampling factor 4. Linear
methods show residual aliasing artifacts due to inaccuracies in the coil
profile reconstructions.
Diffusion-MRI allows measurements of the diffusion of water molecules, which are described in some approximation by a 6 dimensional Fourier transform. In the brain diffusion mainly takes place along nerve fibers. Classically, diffusion in each voxel is modelled by a tensor, which is determined by 7 measurements. For reconstructing fiber tracks, this approach leads to difficulties at fiber crossings. A way out is the use of High Angular Resolution Diffusion Imaging (HARDI). The aim is to reconstruct the diffusion strength at each voxel and in each direction. Hence, the unknown orientation distribution function depends on three spatial and two angular variables. In the PhD thesis of Christoph Ruegge we studied special regularization terms which only enforce smoothness along fibers, but not orthogonal to the fibers. By studying the functional analytic properties of the corresponding norms we could in particular establish the regularizing property of the approach.

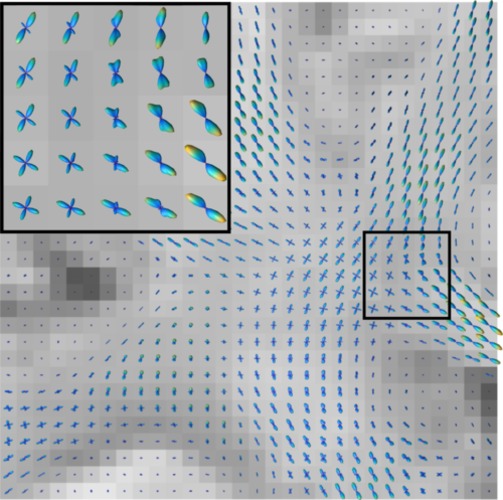
Reconstruction of the location- and direction-dependent probability of
diffusion in an in-vivo data set in a region with crossing fibers close to
the corpus callosum. The glyphs in each voxel are extended in direction with
higher diffusion, along the nerve fibers.
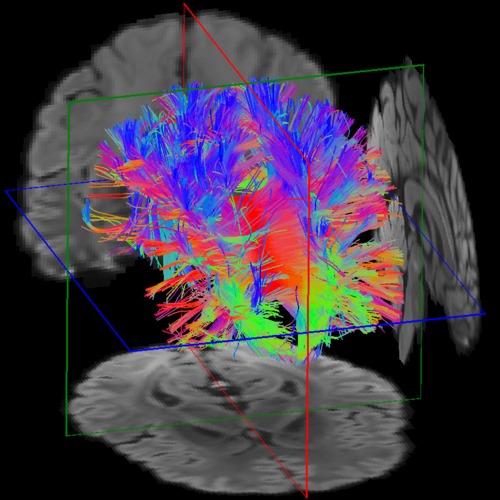
With the help of orientation distribution functions one can reliably reconstruct fiber tracks even in the presence of crossings. In the PhD thesis of Helen Schomburg we have developed a Bayesian-type semi-local tracking algorithm, in which noise sensitivity is substantially reduced by a combination of extrapolation and a look-ahead strategy. In a stochastic variant we additionally obtain information on the uncertainty of our tracking results.


Fiber tracking based on ODF reconstructions. Left: Section of the centrum
semiovale, right: tractography of the corpus callosum starting in the middle
sagittal slice of the volume data.
Currently we are working with Martin Uecker on 2 and 3 dimensional real-time cardiac MRI.

applications