X-ray phase contrast imaging
Classical X-ray radiography, as applied in medical imaging, measures the amount of absorption experienced by X-rays traversing an unknown object. The shadow images obtained by this non-invasive technique may for instance reveal anomalities in interior organs or fractures in bones of human patients.
The advantage of X-rays compared to visible light lies in their short wavelength, allowing - in principle - for nanometer resolution, and in the partial transparency of biological tissue to the former radiation. However, the latter aspect also constitutes a major difficulty when it comes to imaging millimeter-, micrometer- or even nanometer-sized objects: thin samples composed mainly soft biological tissue or - more generally - of light-element materials, are simply too transparent to yield sufficient contrast, i.e. to give rise to an actual shadow in the recorded X-ray image.
A remedy is given by phase contrast imaging, based on the refraction of X-rays: as coherent X-rays traverse matter, their wave fronts propagate faster than in vacuum, resulting in a phase shift at the object's exit surface that is proportional to the projected electron density along the ray path (see sketch in Figure 1). This effect may be up to 1000-times stronger than the absorption and thus enables improved contrast. However, the phase shifts cannot be observed directly but have to be numerically reconstructed from the intensity patterns recorded by a detector placed a few meters behind the sample. It is the diffraction of the propagating X-ray wave field that encodes some of the sought phase information into measurable intensities. This diffraction process has to be mathematically inverted to retrieve phase contrast images.
As demonstrated by Figure 2, showing the measured hologram as well as the reconstructed phase image of an ensemble of Deinococcus radiodurans bacteria, phase contrast enables X-ray imaging of quasi-transparent micro- and nanoscale specimen. Our aim is to promote this promising imaging technique by mathematical analysis of the involved image reconstruction problem and tailored algorithms. In particular, our research addresses the following problems:

Figure 1: Schematic setup of propagation-based phase contrast imaging: coherent incident X-rays traverse an unknown object, encoding its structure as refractive phase shifts in the wave field, which are indirectly measured by the resulting diffraction pattern at a downstream detector.

Figure 2: Phase contrast image (right) of an ensemble of Deinococcus radiodurans bacteria, reconstructed by regularized Newton methods (IRGNM) from intensity data (left) recorded at GINIX endstation , P10-beamline, DESY.
Image reconstruction from Poisson data
In photonic imaging the measurements are given by counts of photons which have interacted with an unknown object of interest. The exact number of incident photons on a specific detector pixel is intrinsically random, only the expected counts can be described by deterministic models. If the interaction is modeled by an operator F then this corresponds to the equation
F(u) = G
where the right-hand side G is a Poisson process , i.e. a random set of points with special properties. The intensity of G (i.e. the total number of points) depends linearly on the observation time t, and as t tents to infinity, we expect 1/t * G to tend weakly to the exact right-hand side g.
Problems of the form described above occur frequently in photonic imaging methods. In particular, we work on the following imaging applications:
The a-priori information on the Poissonian distribution of the random variable G should be taken into account when trying to reconstruct u. Especially if the observation time t is small, ignoring the distribution of G will lead to uncompetitive reconstructions.
Classical X-ray radiography, as applied in medical imaging, measures the amount of absorption experienced by X-rays traversing an unknown object. The shadow images obtained by this non-invasive technique may for instance reveal anomalities in interior organs or fractures in bones of human patients.
The advantage of X-rays compared to visible light lies in their short wavelength, allowing - in principle - for nanometer resolution, and in the partial transparency of biological tissue to the former radiation. However, the latter aspect also constitutes a major difficulty when it comes to imaging millimeter-, micrometer- or even nanometer-sized objects: thin samples composed mainly soft biological tissue or - more generally - of light-element materials, are simply too transparent to yield sufficient contrast, i.e. to give rise to an actual shadow in the recorded X-ray image.
A remedy is given by phase contrast imaging, based on the refraction of X-rays: as coherent X-rays traverse matter, their wave fronts propagate faster than in vacuum, resulting in a phase shift at the object's exit surface that is proportional to the projected electron density along the ray path (see sketch in Figure 1). This effect may be up to 1000-times stronger than the absorption and thus enables improved contrast. However, the phase shifts cannot be observed directly but have to be numerically reconstructed from the intensity patterns recorded by a detector placed a few meters behind the sample. It is the diffraction of the propagating X-ray wave field that encodes some of the sought phase information into measurable intensities. This diffraction process has to be mathematically inverted to retrieve phase contrast images.
As demonstrated by Figure 2, showing the measured hologram as well as the reconstructed phase image of an ensemble of Deinococcus radiodurans bacteria, phase contrast enables X-ray imaging of quasi-transparent micro- and nanoscale specimen. Our aim is to promote this promising imaging technique by mathematical analysis of the involved image reconstruction problem and tailored algorithms. In particular, our research addresses the following problems:

Figure 1: Schematic setup of propagation-based phase contrast imaging: coherent incident X-rays traverse an unknown object, encoding its structure as refractive phase shifts in the wave field, which are indirectly measured by the resulting diffraction pattern at a downstream detector.

Figure 2: Phase contrast image (right) of an ensemble of Deinococcus radiodurans bacteria, reconstructed by regularized Newton methods (IRGNM) from intensity data (left) recorded at GINIX endstation , P10-beamline, DESY.
Image reconstruction from Poisson data
In photonic imaging the measurements are given by counts of photons which have interacted with an unknown object of interest. The exact number of incident photons on a specific detector pixel is intrinsically random, only the expected counts can be described by deterministic models. If the interaction is modeled by an operator F then this corresponds to the equation
F(u) = G
where the right-hand side G is a Poisson process , i.e. a random set of points with special properties. The intensity of G (i.e. the total number of points) depends linearly on the observation time t, and as t tents to infinity, we expect 1/t * G to tend weakly to the exact right-hand side g.
Problems of the form described above occur frequently in photonic imaging methods. In particular, we work on the following imaging applications:
The a-priori information on the Poissonian distribution of the random variable G should be taken into account when trying to reconstruct u. Especially if the observation time t is small, ignoring the distribution of G will lead to uncompetitive reconstructions.
|
|
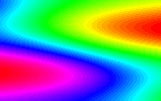
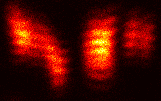
| Figure 3: Relative phase occuring in 4Pi microscopy | Figure 4: Simulated data for the 4Pi problem |
|
|
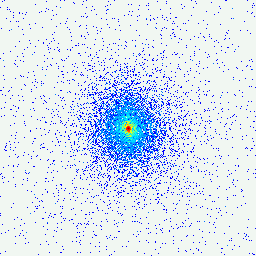
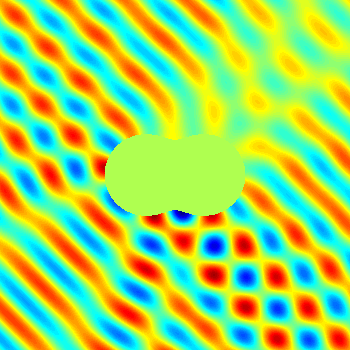
| Figure 5: Simulated data for a phase retrieval problem | Figure 6: Real part of the total field for an inverse obstacle scattering problem |

applications